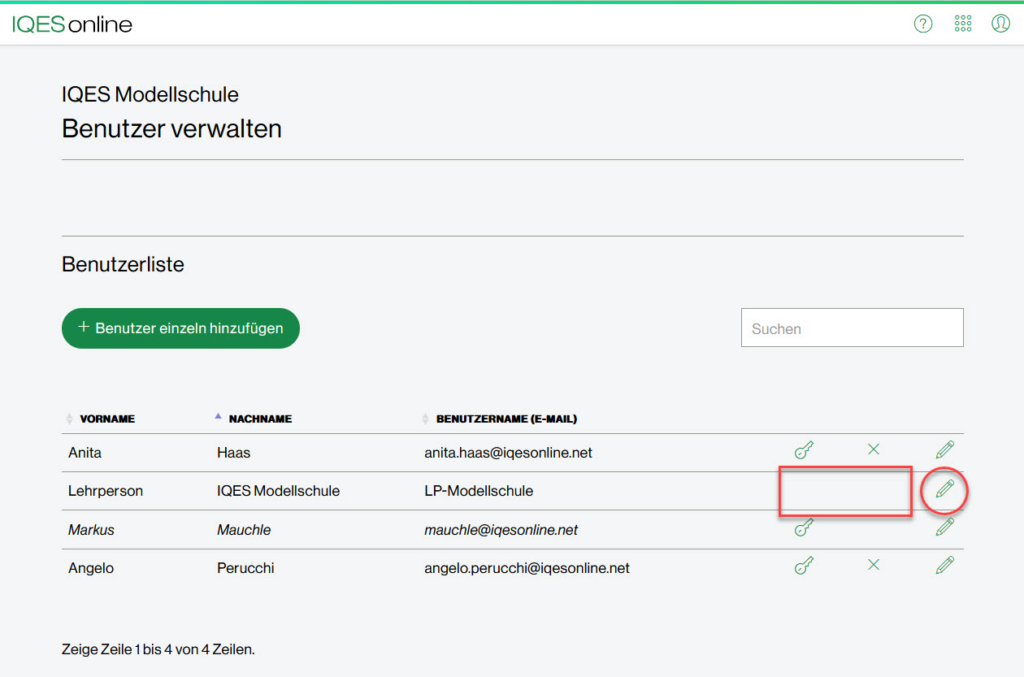
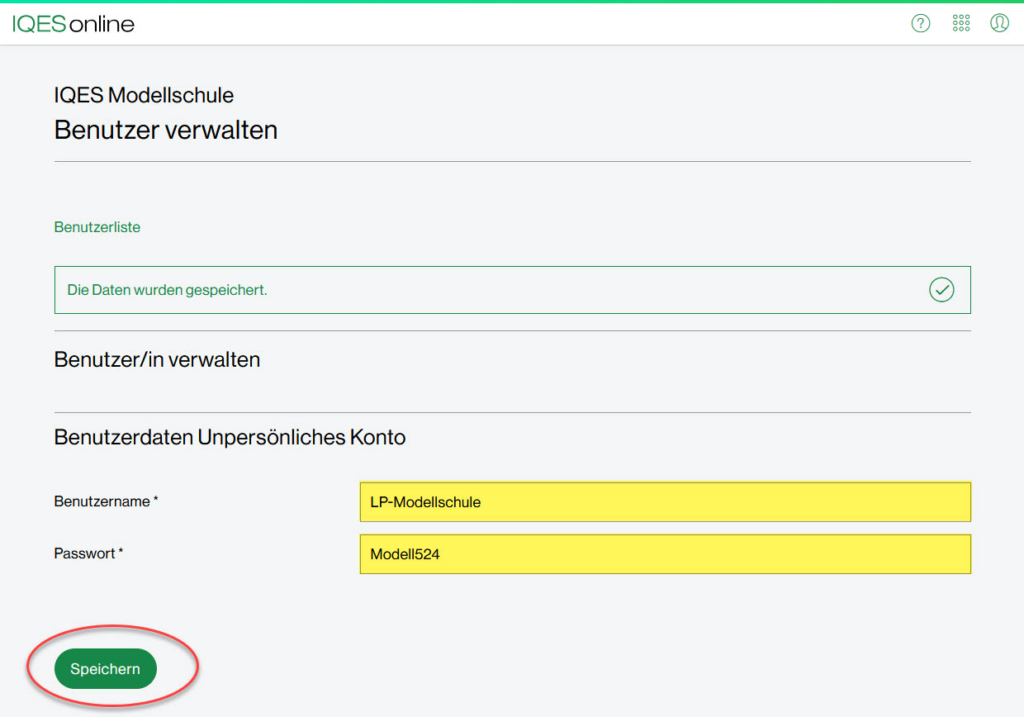
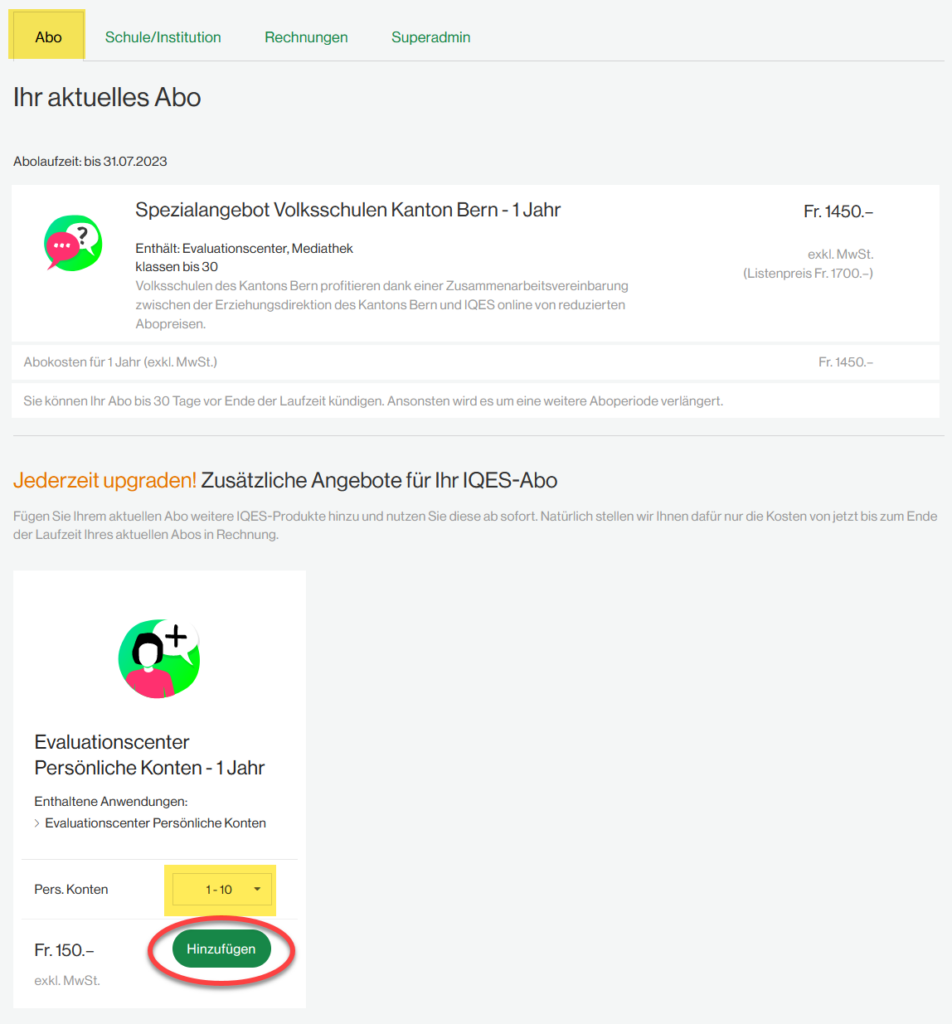
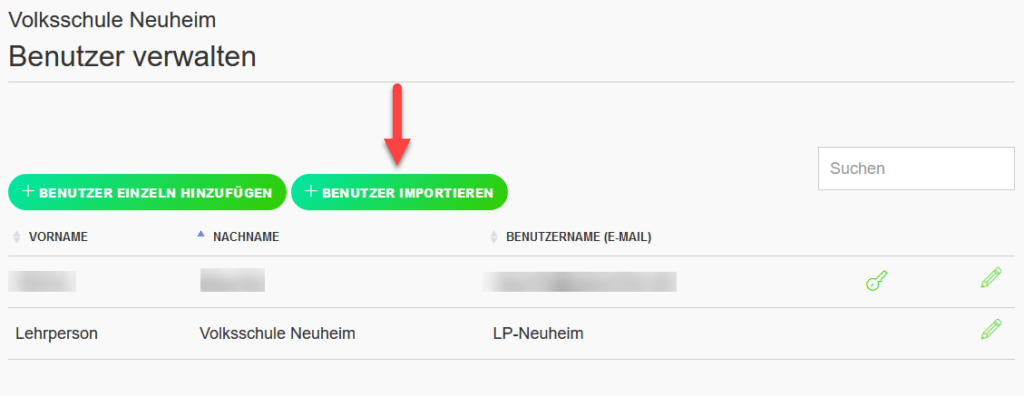
Einleitung – Mathematik 5:
vereint die mathematischen Grundlagen des Mathematikunterrichts der 5. Jahrgangsstufe in einzelnen Lernumgebungen. Die Lernumgebungen sind nach inhaltlich zusammenhängenden Themengebieten aufgebaut und bieten eine Vielzahl an Möglichkeiten zur Umsetzung im Unterricht.
Lernumgebungen für einen zeitgemäßen, kompetenzorientierten Unterricht
Die Lernumgebungen Mathematik für die 5. Klasse bieten eine große Auswahl an differenzierenden Übungsaufgaben und ermöglichen individuelle Lernwege. Nach Niveaustufen gegliederte Lerntests bilden die Grundlage für eine formative Selbst- und/ oder Fremdeinschätzung. Je nach Lernstand können Schüler*innen anschließend mit Hilfe von Rückspiegelaufgaben Lücken schließen und Themen weiter vertiefen. Weiter steht den Lehrpersonen ein großer Pool an nach Niveaustufen differenzierten Aufgaben zur Verfügung, um einen das Themengebiet abschließenden Test passend zu gestalten.
Lernumgebungen in einem sinnvollen thematischen Aufbau
Die Lernumgebungen sind nach einem logischen Aufbau der einzelnen mathematischen Themen gegliedert, sind aber natürlich auch frei wählbar, – auch über die hier vorgenommene thematische Zuordnung zur Jahrgangsstufe 5 hinaus. Die Lernumgebungen können auch in veränderter Reihenfolge oder anderen Klassenstufen eingesetzt werden, – je nach leitenden Lehr- und Bildungsplänen, eingesetzten klassischen Lehrmitteln und individuellen Setzungen einer Lehrperson. Alle Materialien können im Zusammenhang oder unabhängig voneinander eingesetzt werden.
Einsatz der Unterrichtsmaterialien
Pädagogischer Einsatz der Lernumgebungen Mathematik 5 und 6
Die Lernumgebungen sind alle gleich aufgebaut und entsprechen durch ihre verschiedenen Unterrichtsphasen und Materialien einem binnendifferenzierenden und kompetenzorientierten Mathematikunterricht. Der wiederkehrende Aufbau und die Kennzeichnung der Materialien mit unterschiedlichen Farben ermöglichen Lehrpersonen und Schülern*innen eine schnelle Orientierung.
Autor/Autorin: Gernot Braun
Umfang/Länge: 6 Seiten
Aus: Lernumgebung Mathematik 5
Fächer: Mathematik
Stufen: 5. Stufe, 6. Stufe
Regeleinträge
Übungsaufgaben und Lösungen
Die Übungsaufgaben starten in der Regel mit einfacheren Einstiegsaufgaben, die alle Schüler*innen lösen können sollten. Die Reihenfolge der Aufgaben unterliegt einem logischen inhaltsbezogenen Aufbau, den man auch im Unterricht berücksichtigen kann, aber nicht immer zwingend muss.
Die einzelnen Aufgabentypen sind jeweils klar formuliert und gehen von eindeutigen Fragestellungen aus. Sie sind Alltagsaufgaben, mit denen die grundlegenden Techniken in der Arithmetik und Geometrie erlernt und gefestigt werden. Im weiteren Verlauf eines Themas finden sich dann auch komplexere und mit anderen Inhalten verknüpfte Aufgaben, sehr viele davon mit realem Alltagsbezug. Auch finden sich offenere oder problemorientierte Aufgaben, bzw. solche, die nur argumentativ gelöst werden können. Der Taschenrechner sollte in der gesamten Lernumgebung noch nicht eingesetzt werden.
Die große Aufgabenfülle sollte keineswegs zur Annahme führen, dass alle Schüler*innen nun alle Aufgaben lösen sollten. Auch werden im Unterricht nicht alle Aufgaben bearbeitet. Vielmehr geht es für die Lehrperson, aber auch die Schüler*innen darum, die Möglichkeit zur individuellen Auswahl zu haben.
Dies ist auch deshalb sehr gut möglich, weil die einzelnen Aufgaben alle mit der Angabe von Sternen in der Schwierigkeitsstufe differenziert sind: * leicht | ** mittel | ***schwierig
Weiter wird bei einer Aufgabenfolge mit zwei Symbolen auch angegeben, wie die Aufgabe zu bearbeiten ist:
- Die Aufgabe sollte direkt auf dem Blatt gelöst werden
- Die Aufgabe muss im Rechenheft/ auf einem Zusatzblatt gelöst werden
- Als zusätzliche Hilfestellungen für selbständiges, freies Arbeiten, gibt die Glühbirne als «Helferlein» Tipps und Hinweise, die von Nutzen sein können.
Die Lösungsblätter zu allen Übungsaufgaben lassen sowohl Selbst- wie auch Fremdkontrolle als methodische Möglichkeiten zur Überprüfung offen.
Lerntests und Lösungen
Die Lerntests A, B und C sind als zwischenzeitliche formative Lernkontrolle des gesamten Kapitels gedacht. Sie sind in drei Schwierigkeitsstufen aufgeteilt, wobei Lerntest C die anspruchsvollste Variante ist.
Die Möglichkeit, mithilfe der Lerntests den eigenen Lernstand genau unter die Lupe zu nehmen, noch vorhandene Lücken zu erkennen und in der Folge mithilfe des Rückspiegels schließen zu können, ist für die Lernmotivation der Schüler*innen von enormer Bedeutung. Die formative Rückmeldung schafft Orientierung und ermöglicht gezielte Weiterentwicklung des persönlichen Lern- und Wissensstandes.
Rückspiegel und Lösungen
Der Rückspiegel eröffnet (nach den Erkenntnissen aus dem Lerntest) die nächsten Lernschritte. Je nach Lernstand können bestimmte mathematische Muster und Konzepte nochmals erkundet, systematisiert und gesichert werden. Der Rückspiegel bietet Aufgaben zum Üben, Vertiefen und Wiederholen an und macht damit eine individualisierte Vorbereitung und Lernbegleitung auf den Abschlusstest möglich
Selbstverständlich ist es auch möglich, alle Schüler*innen noch einmal durch das gesamte Kapitel Übungsaufgaben lösen zu lassen; der Rückspiegel bietet sich aber als individuelle Auswahl geradezu an.
Aufgabenpool für Abschlusstests und Lösungen
Auch diese Aufgabensammlung ist als Auswahl gedacht. Lehrpersonen können damit einen eigenen, auf den Lernstand der Klasse zugeschnittenen Abschlusstest zusammenstellen und auf diese Weise den Leistungsstand der einzelnen Schüler*innen und der ganzen Klasse summativ beurteilen.
Einbettung in eine Unterrichtsreihe
Die Unterrichtsmaterialien der Lernumgebungen können im Verbund mit klassischen Lehrmitteln und eigenen Lehr- und Lernmaterialien verwendet werden.
Unterrichtsphasen | Unterrichtsmaterial dieser Lernumgebung | Eigene Lehr- und Lernmaterialien |
|---|---|---|
Einstieg und Orientierung | Kompetenzorientierte Lernziele (als Orientierung für die Schüler*innen) Kompetenzbogen mit «Ich kann …»-Formulierungen zur Selbsteinschätzung | Informierender Einstieg Direkte Instruktion Diagnose Vorwissen und Lernvoraussetzungen |
Erkunden und Erarbeiten | mit ausgewählten Aufgaben aus der Lernumgebung Schüler*innen probieren eigene Lösungswege aus, entdecken selbst Strategien und vergleichen diese in kooperativen Lernsituationen | Offene Einstiegsaufgaben in freier Arbeitsweise Adaptive Lernbegleitung, Coaching, gezieltes Feedback und Anleitung durch Lehrperson |
Systematisieren und Sichern | Regeleinträge – Basiswissen – Erklärvideos | Lerngerüste Erklärungen und direkte Instruktion |
Üben | Zuteilung von differenzierenden Lernangeboten: Übungsaufgaben auf drei Niveaustufen (jeweils in ohne oder mit Lösungen) | |
Vertiefen und Wiederholen | Lerntest (formative Lernkontrollen auf drei Niveaustufen, jeweils ohne oder mit Lösungen) Rückspiegel (Aufgabensammlung zur Vertiefung und Wiederholung) | |
Anwenden, Überprüfen und Bewerten | Abschlusstest (Aufgabenpool zur Auswahl für die Lehrperson) Bilanzierende Selbst- bzw. Fremdbeurteilung mit Kompetenzbogen |
Weniger ist mehr – Verstehen, Vertiefen und Anwenden ist zentral
Die Aufgabensammlungen sollen nicht dazu verleiten, möglichst viele Aufgaben abarbeiten zu lassen. Wie meist in nachhaltigen Lernprozessen ist weniger mehr. Eine vertiefte Auseinandersetzung mit Aufgaben und den darin zu entdeckenden mathematischen Mustern und Zusammenhängen ist in jedem Fall einer fleißigen und oberflächlichen Erledigung einer Flut von Aufgaben vorzuziehen. Ziel eines schülerzentrierten Unterrichts ist die optimale Passung von Aufgaben und Lernvoraussetzungen.
Differenzierende Lernaufgaben, die es Schüler*innen ermöglichen, diese auf unterschiedlichen Niveaus zu bearbeiten, verhindern Unter- und Überforderung. Sie ermöglichen ein Lernen in der «Zone der nächsten Entwicklung» (Vygotsky 1978) und damit optimale Lernfortschritte.